1D Wärmeleitung
Heute haben wir ein heißes Filmchen von beweglichen Kurven für euch.
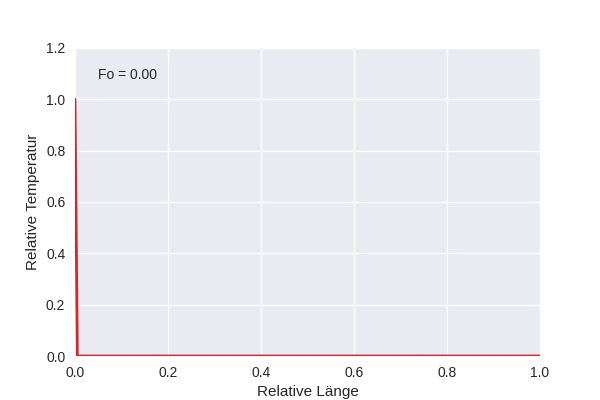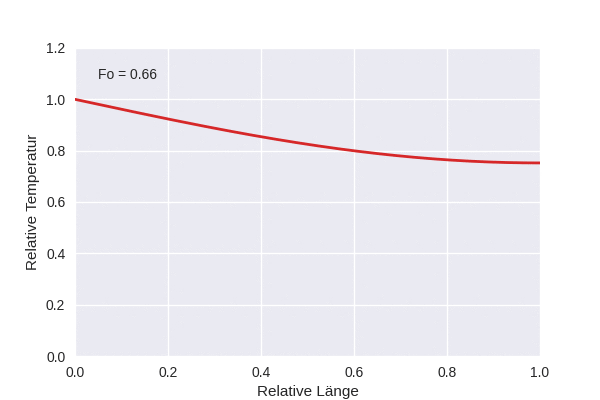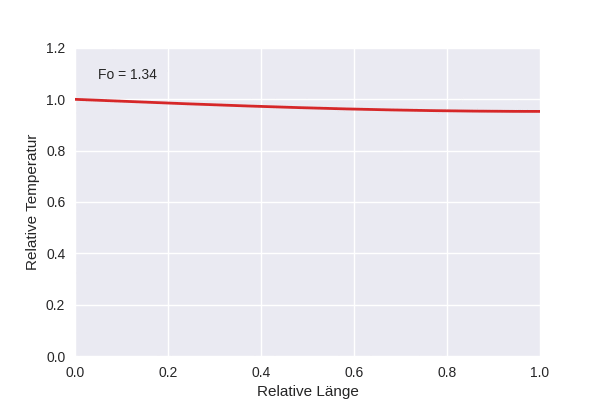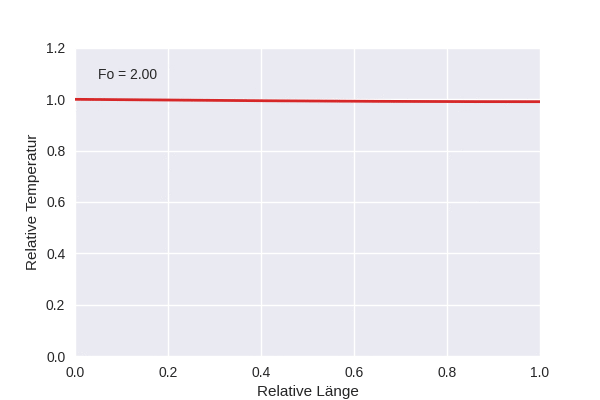
Die Animation zeigt die Temperaturentwicklung in einem eindimensionalen Gebiet, wenn am linken Rand eine feste Temperatur \(T_1\) anliegt, die Anfangstemperatur \(T_0\) konstant war, und der rechte Rand für Wärmefluss geschlossen ist, also \(\partial T/\partial x (x=1,t) = 0\).
In der Animation ist die relative Temperatur dargestellt:
\[\tau = \frac{T - T_0}{T_1 - T_0}\]
Die Länge \(x\) ist ebenfalls auf die Länge des Gebiets \(L\) normiert, und als Zeit wird die dimensionslose Fourier-Zahl verwendet,
\[\text{Fo } = \frac{\alpha t}{L^2}\]
wobei \(\alpha\) die Wärmediffusivität ist.
\(\tau\) erfüllt die Wärmeleitungsgleichung, die mit den gegebenen Randbedingung durch einen Separationsansatz gelöst werden kann. Das Ergebnis ist die Reihe
\[\tau(x, \text{Fo}) = 1 - \frac{4}{\pi}\sum\limits_{n=1}^{\infty}\frac{1}{2n-1}\, \sin\left(\frac{(2n-1)\pi}{2}x\right)\, \exp\left(-(2n-1)^2\pi^2\frac{\text{Fo}}{4}\right)\]
Der Exponentialterm geht sehr schnell gegen 0, weshalb die Reihe für \(\text{Fo } > 0\) konvergiert, und näherungsweise durch eine endliche Partialsumme berechnet werden kann. Zur Abschätzung der Größenordnung des dabei entstehenden Näherungsfehlers kann der Betrag des letzten berücksichtigten Summands genutzt werden.
Für \(\text{Fo } = 0\) und \(x > 0\) konvergiert die Reihe gegen \(\pi/4\), der Beweis ist wie immer dem Leser als Übungsaufgabe überlassen (Hinweis: Fourierreihe des Rechteckpulses). Allerdings ist die Konvergenz deutlich langsamer, weshalb eine Berechnung der Reihe nicht sinnvoll ist.
Eine Implementation der Temperaturberechnung in Python könnte so aussehen:
from itertools import takewhile, count
from math import pi, sin, exp
def tau(x, Fo, eps=1e-10):
"""
Calculate relative temperature at relative position x and dimensionless
time Fo up to given precision.
"""
if Fo == 0:
return float(x == 0)
else:
return 1 - 4/pi * sum(
takewhile(
lambda a: abs(a) > eps,
map(
lambda n:
sin((2*n - 1) * pi/2 * x)
/ (2*n - 1)
* exp(-(2*n - 1)**2 * pi**2 * Fo/4),
count(1)
)
)
)