Savage Worlds-Statistik
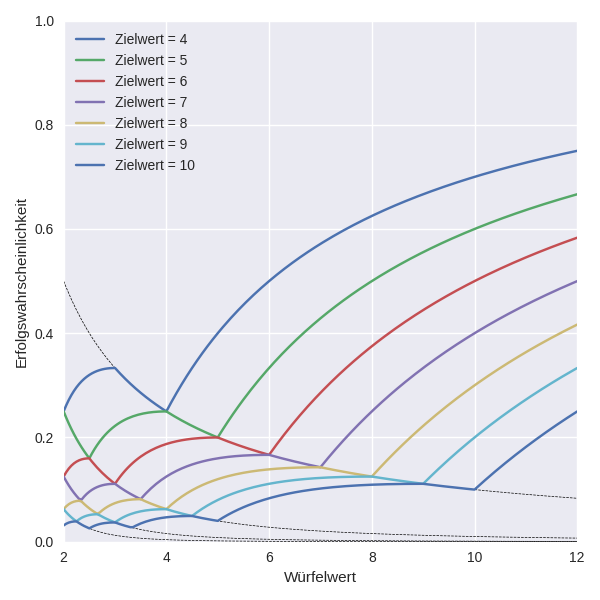
Obige Abbildung zeigt die Erfolgswahrscheinlichkeiten für Fertigkeitsproben mit verschiedenen Würfel- und Zielwerten bei Savage Worlds. Überraschenderweise steigen die Linien nicht monoton mit dem Würfelwert an. Warum das so ist, wird im Folgenden genauer erklärt.
Savage Worlds ist ein Pen&Paper-Rollenspielsystem, ähnlich wie Dungeons and Dragons (DnD) oder Pathfinder. Einer der größten mechanischen Unterschiede von Savage Worlds zu DnD und Pathfinder zeigt sich in der Art, wie Fertigkeitsproben durchgeführt werden. Bei DnD und Pathfinder werden diese stets mit einem W20 geworfen, wobei je nach Erfahrung in der getesteten Fertigkeit Boni oder Mali zum Wurfergebnis hinzugezählt werden. Bei Savage Worlds wird stattdessen der Würfel je nach Erfahrung angepasst: Je höher die Erfahrung, desto höherwertiger der Würfel.
Zusätzlich können Würfel bei Savage Worlds explodieren, wenn ein Ass, also der höchstmögliche Würfelwert, gewürfelt wurde. In diesem Fall darf man nochmal würfeln, und zählt den neuen Wert zum vorherigen Wert hinzu. Dies kann so oft wie möglich wiederholt werden, Würfel können also unter Umständen mehrfach explodieren. Dadurch kann z.B. auch mit einem W4 eine Fertigkeitsprobe mit Zielwert 6 geschafft werden.
Das Explodieren verändert die gewöhnliche Gleichverteilung von Würfelergebnissen. Dadurch profitieren insbesondere kleine Würfel, da bei ihnen die Wahrscheinlichkeit auf ein Ass recht hoch ist. Deshalb ist a priori nicht ausgeschlossen, dass es Konstellationen gibt, in denen ein höherer Würfel die Wahrscheinlichkeit senkt, eine Fertigkeitsprobe zu bestehen.
Um diese Frage zu klären, betrachten wir zunächst die Wahrscheinlichkeitsverteilung der Würfelergebnisse. Diese ist
\[\text{Pr}_d(X=x) = \begin{cases} d^{-\left\lfloor\frac{t}{d}\right\rfloor}&\quad \text{wenn } x \text{ mod } d \neq 0\ 0&\quad\text{sonst}\end{cases}\]
Dabei ist \(d\) der Nennwert des Würfels. Dieser kann nicht erreicht werden, da die Würfel bei diesen Werten explodieren. Basierend auf dieser Wahrscheinlichkeitsverteilung kann der Erwartungswert eines Wurfs berechnet werden:
\[\begin{alignat}{2}
\mathrm{E}d[X] &= \sum\limits{i=1}^{d-1} \frac{i}{d} + \frac{1}{d} \cdot
\left[\sum\limits_{i=1}^{d-1}\frac{d+i}{d} + \frac{1}{d}
\left(\sum\limits_{i=1}^{d-1}\frac{2d+i}{d} + …\right)\right]
&= \sum\limits_{k=0}^{\infty}\sum\limits_{i=1}^{d-1} \frac{kd+i}{d^{k+1}}
&= \sum\limits_{k=0}^{\infty}\sum\limits_{i=1}^{d-1} \left(\frac{k}{d^k} + \frac{i}{d^{k+1}}\right)
&= (d-1)\cdot\sum\limits_{k=0}^{\infty}\frac{k}{d^k} + \frac{d(d-1)}{2}\sum\limits_{k=1}^{\infty}\left(\frac{1}{d}\right)^k
&= (d-1)\cdot\frac{d}{(1-d)^2} + \frac{d(d-1)}{2}\cdot \frac{1}{d-1}
&= \cdot\frac{2d+d^2-d}{2(d-1)}
&= \frac{d + 1}{2}\cdot\frac{d}{d-1}
\end{alignat}\]
Der erste Term entspricht dem Erwartungswert bei normalen Würfelwürfen. Der zweite Term ensteht aus der Modifikation durch explodierende Asse. Dieser zweite Term ist besonders bei kleinen Würfeln groß, weshalb diese überproportional stark davon profitieren. Für \(d\geq4\) (W4 und größer) steigt der Erwartungswert aber monoton an.
Die folgende Abbildung zeigt die Wahrscheinlichkeiten für Savage Worlds Würfelergebnisse mit explodierenden Assen, sowie Erwartungswert und 10%- bzw. 90%-Perzentile für verschiedene Würfel. Zum Vergleich des Explosionseffekts ist ebenfalls der Erwartungswert ohne Explosion dargestellt.
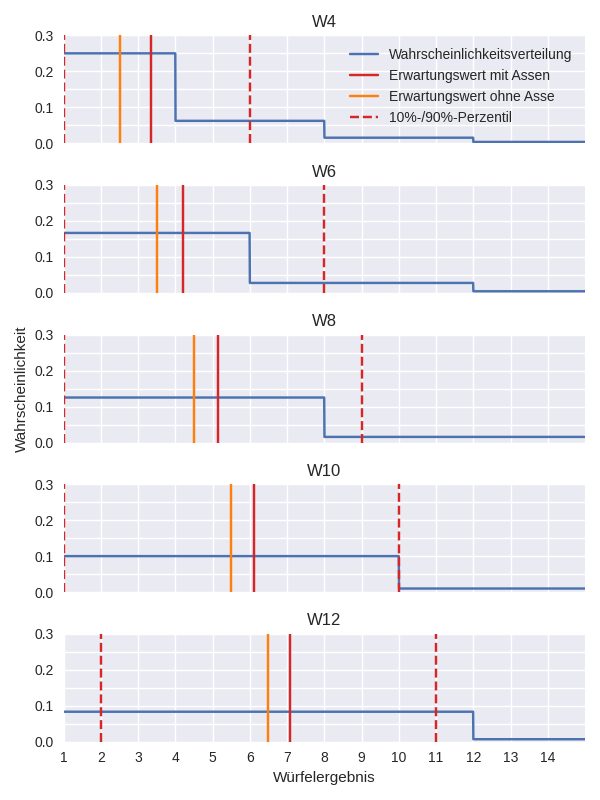
Um die tatsächliche “Würfelperformance” auszuwerten ist der Mittelwert allerdings nicht geeignet. Sinnvoller ist es, die Erfolgswahrscheinlichkeit für einen Zielwert \(t\) zu betrachten. Diese kann mit
\[\text{Pr}d(X\geq t) = \left(\frac{1}{d}\right)^n \cdot \left(1 - \frac{(r - 1)+}{d}\right)\]
berechnet werden, wobei
\[\begin{alignat}{2}
n &= \left\lfloor\frac{t}{d}\right\rfloor
r &= t\text{ mod } d.
\end{alignat}\]
(Der Beweis ist dem Leser als Übungsaufgabe überlassen.)
Der Zielwert bei Savage Worlds Fertigkeitsproben ist meist 4, allerdings kann dieser durch besondere Umstände verändert werden, meist indem vom Wurfergebnis eine feste Punktzahl abgezogen wird. Dies ist analog zu einer Erhöhung des Zielwerts. Das Ergebnis ist die erste Abbildung dieses Beitrags.
Dort ist zunächst zu beachten, dass die Erfolgswahrscheinlichkeiten hier auch für nicht-ganzzahlige Würfel aufgetragen sind, indem in obiger Formel naiv reelle Würfelwerte eingesetzt wurden. Die Kurven für feste Zielwerte \(t\) sind zwar stetig, weisen aber Knicke auf. Diese Knicke treten bei \(d=t\), \(t-1\), \(t/2\), \((t-1)/2\), … auf. Dabei ist der Wert bei \(d=t\) stets geringer als bei \(d=t-1\), d.h. in diesem Bereich sinkt die Erfolgswahrscheinlichkeit mit steigendem Würfelwert!
Für das tatsächliche Spiel hat dieser Fall keine Auswirkungen, da nur gerade Würfel verwendet werden. Allerdings sind selbst bei Würfelwert \(d = t-2\) die Erfolgswahrscheinlichkeiten noch leicht gegenüber \(d = t\) erhöht, besonders bei Zielwert 6: Hier ist die Erfolgswahrscheinlichkeit mit einem W4 höher als mit einem W6. In Zahlen: die Erfolgswahrscheinlichkeit mit W4 ist \(3/16 = 18,75%\), mit W6 ist sie \(1/6 \approx 16,67%\).
Die durchgezogene Linie von \(d=t-1\) zu \(d=t\) zeigt noch ein weiteres überraschendes Verhalten: Die Linien von aller Zielwerte ergänzen sich zu einer Linie. Die anderen Linien zeigen das selbe Verhalten. Diese “schneidenden” Linien stimmen mit \(1/d\), \(1/d^2\), … überein.