Posts
-
Die gehobene Kunst der Kritzelei
Heute zeige ich euch, wie man auf äußerst elegante Art und Weise, Kunstwerke von 2 bis 3 jährigen Menschen imitiert. Hierzu trainieren wir ein Neuronales Netzwerk. Obwohl das jetzt richtig abgefahren klingt, ist das nichts anderes wie ein gutes Minimum einer speziellen Funktion \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) mit einer Optimierungsmethode zu finden. Doch wieder abgefahren ist aber, dass \( n \) oft größer \(10^6\) ist.
Die Optimierungsmethode folgt also einem Pfad von einem Startpunkt zu einem Minimum auf einer circa \(10^6\) dimensionalen Funktion. Kann man sich jetzt schwer vorstellen, aber stellt euch einfach einen Pfad in 3 Dimensionen vor und glaubt dabei ganz fest daran, dass es noch 999997 weitere Richtungen gibt. Nun projizieren wir den Pfad, auf die Länge jedes Schrittes und erhalten dabei die Winkel zwischen aufeinanderfolgenden Schritten.
Als Ergebnis erhalten wir je nach Optimierungsmethode wunderschöne Krizeleien: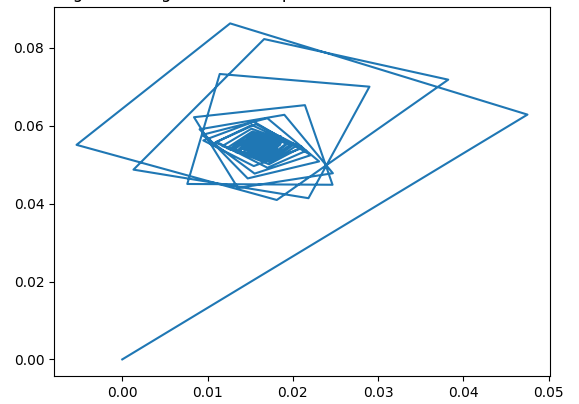
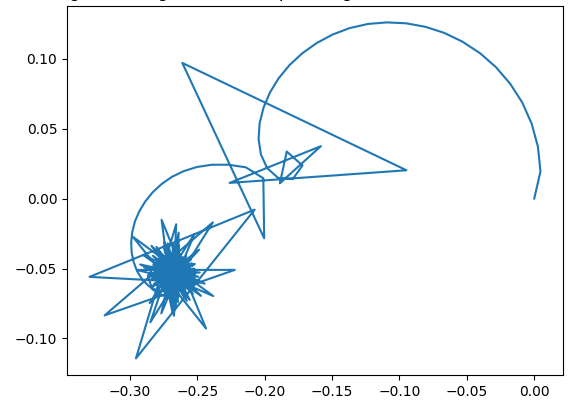
Pfade von Trainings eines Neuronalen Netzwerks mit einer Liniensuche (links) und mit Gradientenabstieg (rechts).
-
Fraktale mit komplexen Polynomen
Heute gibt es tiefe Einblicke in ästhetische (geometrische) Körper.

Wir betrachten ein Polynom \( p \) auf der komplexen Ebene mit
\[ p(z)= {435.147z^{3.2683} -270.845z^{-8.289} -936.558} \]
Ein sehr einfaches Verfahren die Nullstellen dieses Polynoms zu berechnen ist die Newton-Methode. Unter den richtigen Umständen konvergiert die Reihe
\[ z_{n+1} = z_n - \frac{p \left( z_{n} \right) }{p’ \left( z_{n} \right) } \]
zu einer (komplexen) Nullstelle des Polynoms \( p \). Dabei muss aber anfangs ein Startwert \( z_0\) geraten werden. Wir wählen für diese Startwerte gleichverteilte Punkte auf der komplexen Ebene, berechnen die Nullstellen mit dem oben genannten Verfahren und stellen den Logarithmus der Anzahl der benötigten Interationen \( n_{\text{iter}} \) um ein vorher festgelegtes Konvergenzkriterium zu erfüllen, mittels einer Farbskala dar.
Im ersten Frame der Animation blicken wir auf die komplexe Ebene mit \( \left( z \in \mathbb{C} : \Re(z) \in \left[ -10,10 \right] , \Im(z) \in \left[ -10 , 10 \right] \right) \) und verkleinern den Bereich langsam auf \( \left( z \in \mathbb{C} : \Re(z) \in \left[ -3.093 \times 10^{-3}, 3.093 \times 10^{-3} \right] , \Im(z) \in \left[ -3.093 \times 10^{-3}, 3.093 \times 10^{-3} \right] \right) \)
Der Algorithmus zeigt ein chaotisches Konvergenzverhalten: Kleine Abweichungen von den “geratenen” Startwerten \( z_0\) führen zu großen Unterschieden in der Anzahl der benötigten Iterationen \( n_{\text{iter}} \).
Mittels Erweiterung des Ableitungsbegriffs auf rationale Ordnungen bekommt man ein anderes Konvergenzverhalten und damit andere Fraktale. So ist z.B. die Riemann-Liouville Ableitung der Ordnung \( \alpha \) eines Monoms \( z^m \) definiert zu:
\[ D^{\alpha}_{\text{RL}} z^m = \frac{\Gamma \left( m+1 \right) }{\Gamma \left( m - \alpha +1 \right)} z^{m-\alpha} \]
mit der komplexen Gammafunktion \( \Gamma \).
Hier gibt’s den Quellcode mit dem das oben gezeigte Fraktal generiert wurde:
-
3d2-Wasserstofforbital
Für alle Liebhaber von engen Löchern gibt es heute eine Iso-p-Fläche des \( 3d_{2} \)-Wasserstofforbitals:

 (neigschaut!)
(neigschaut!)Die Wahrscheinlichkeit das Elektron in einem infinitesimal kleinen Volumenelement in Kugelkoordinaten um das Proton herum zu finden, ist gegeben zu:
\[ p(\rho,\theta,\phi)= { \left| \frac{1}{162\sqrt{\pi}}e^{-\rho/3}{\rho}^2{\sin{(\theta)}}^2e^{2i\phi} \right|}^2, \]
wobei Distanzen \(\rho = r/a_0\) mit dem Bohrschen Atomradius \(a_0\) normiert wurden. Gezeigt wird nur ein Ausschitt der vollen Iso-p-Fläche, die in voller Schönheit einen Torus darstellt.
-
1D Wärmeleitung
Heute haben wir ein heißes Filmchen von beweglichen Kurven für euch.
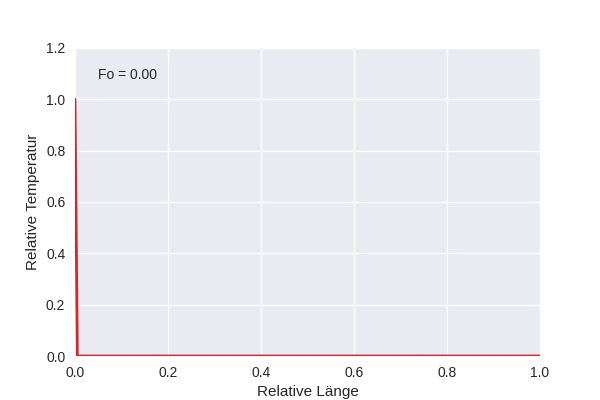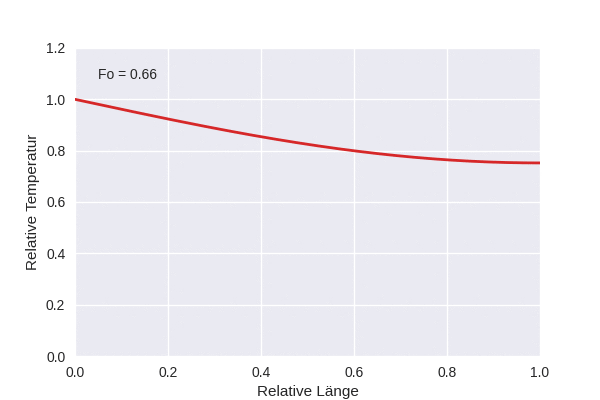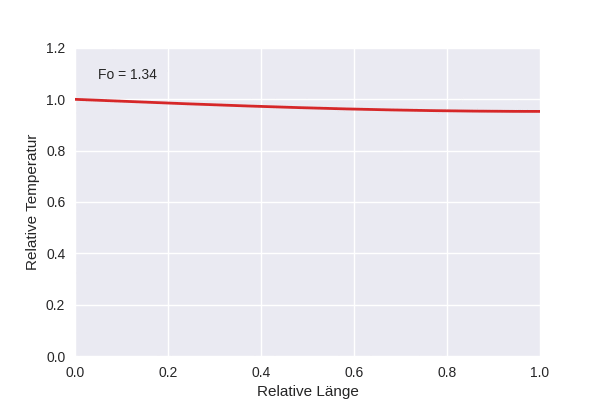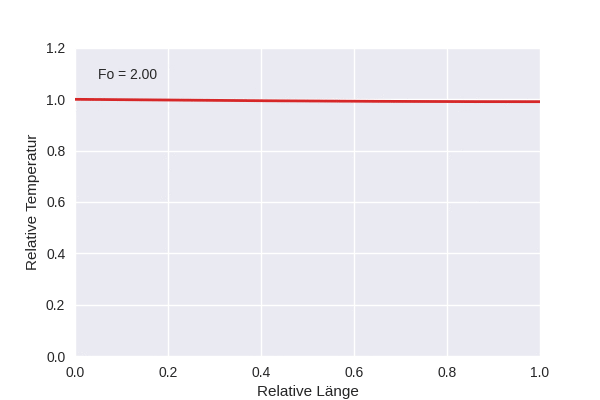
Die Animation zeigt die Temperaturentwicklung in einem eindimensionalen Gebiet, wenn am linken Rand eine feste Temperatur \(T_1\) anliegt, die Anfangstemperatur \(T_0\) konstant war, und der rechte Rand für Wärmefluss geschlossen ist, also \(\partial T/\partial x (x=1,t) = 0\).
-
Savage Worlds-Statistik
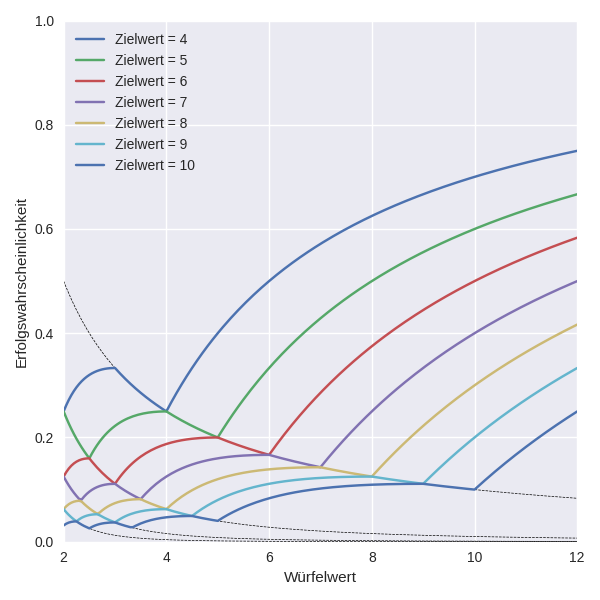
Obige Abbildung zeigt die Erfolgswahrscheinlichkeiten für Fertigkeitsproben mit verschiedenen Würfel- und Zielwerten bei Savage Worlds. Überraschenderweise steigen die Linien nicht monoton mit dem Würfelwert an. Warum das so ist, wird im Folgenden genauer erklärt.
-
Doppelglocke
Heute haben wir eine ganz besondere Funktion für unsere Freunde doppelter Glockenkurven:
\[\text{g}(x,y) = \exp\left(-\frac{((x-4)^2 + (y-4)^2)^2}{1000}\right) + \exp\left(-\frac{((x+4)^2 + (y+4)^2)^2}{1000}\right)\ + 0.1\cdot\exp\left(-((x+4)^2 + (y+4)^2)^2\right) + 0.1 \cdot \exp\left(-((x-4)^2 + (y-4)^2)^2\right)\]

-
Sinus cardinalis
Für alle die auf enge Spalten stehen präsentieren wir heute den Sinus Cardinalis:
\[\text{sinc}(x) = \frac{\text{sin}(x)}{x}\]

subscribe via RSS